Inspiré en partie de l'article de Wes Sonnenreich, Return On Security Investment (ROSI) – A Practical Quantitative Model, Journal of Research and Practice in Information Technology, Vol. 38, No. 1, February 2006. Voir le lien : return_on_security_investment.pdf.
La plupart d'entre nous connait plus ou moins ce que c'est le ROI (Return On Investment = Retour Sur Investissement), élément représentant un facteur financier parmi d'autres fréquemment étudié et analysé avant de se lancer dans un projet nécessitant des investissements. Par contre, il est moins commun de parler de ROSI (Return On Security Investment = Retour Sur Investissement de sécurité) en entreprise. Par ailleurs, ces deux éléments sont aussi utilisés par les éditeurs de logiciels et de solutions technologiques pour mettre en avant les arguments afin de convaincre leurs clients.
Commençons par le plus simple, le ROI dont les formules équivalentes sont :
![]()
![]()
![]()
La dernière formulation indique bien que le ROI est un coefficient (financier) qui peut être positif, négatif ou nulle avec une conclusion appropriée :
| • ROI>0 : | Le projet couvre les investissements et rapporte des gains , donc il peut être rentable (ceci dépend de la valeur du ROI entre autres) |
| • ROI=0 : | Le projet ne rapporte pas de gains, mais il couvre les d'investissements. |
| • ROI<0 : | Le projet ne rapporte pas de gains et il est déficitaire. |
Il est à noter qu'il ne s'agit en aucun cas de confirmation de la conclusion, mais uniquement de prédiction si les hypothèses et les chiffres avancés seront confirmés. Remarquons qu'il est nul part indiqué dans la formulation mathématique la dépendance du ROI du temps, bien qu'il soit exprimé en tant que ratio d'argents investis ou gagnés sur une certaine période de temps à des moments différents. En réalité, il existe une dépendance avec le temps, car les investissements peuvent être réalisés au début, en cours ou à la fin du projet et les gains peuvent être constatés à des repères temporels différents, généralement à la fin d'une année fiscale ou une période planifiée.
D'une manière générale, le ROI est planifié sur une certaine période selon le planning projet qui varie de 1 an à 3 ans, voire 5 ans ou plus et il est exprimé en % pour indiquer le niveau du rendement des gains nets par rapport aux investissements. Un exemple est plus parlant, en voici un :
Exemple 1 : Une société lance une nouvelle gamme de produit à commercialiser. Pour cela, elle prévoit procéder au lancement d'une phase projet sur 3 mois avec un coût d'investissement estimé à 250K€, puis une phase de mise sur le marché qui requiert un investissement de 50K€ sur 3 mois et finalement un investissement de 100K€ pour une production sur les 6 mois restants de l'année planifiée. Sur cette dernière phase des gains issus directement de la vente du nouveau produit sont estimés à 1M€. Quel est le ROI escompté sur 1 an. En appliquant la formule du ROI, on a :
![]()
Ceci signifie que le projet est susceptible de rapporter une fois et demi l'investissement total. On voit bien que le résultat sera le même si les investissements ont lieu à des moments différents à l'intérieur de la période de calcul du ROI. Si on suppose que l'année suivante on a dépennsé un montant proportionnel au coût de production des 6 mois précédents et dont la vente a rapporté 2M€, alors le ROI sur les 2 ans est de :
![]()
La mission du ROI est de dire combien des investissements vont rapporter au bout d'une certaine période peu importe à quel moment ceux-ci auront lieu ? Pour prendre le temps en compte d'autres métriques peuvent être analysés comme la NPV et le IRR (voir la suite de cet article).
Aussi bien les investissements planifiés que les gains escomptés ne sont pas assurés et dépendent d'un certain nombre de facteurs notamment sur de longues périodes sans pour autant que le facteur d'incertitude soit trop important à condition que l'entreprise possède une certaine maîtrise des coûts et dispose d'une bonne santé financière. Que dire alors si les éléments concernés par les investissements ne sont pas du tout contrôlés par l'entreprise ou leur arrêt de fonctionnement, voire leur destruction totale peut avoir un impact majeur sur le business même de l'entreprise. Ceci est tout-à-fait possible notamment dans le domaine de la sécurité de l'informatique, des locaux ou des moyens matériels ou humains. Afin de garantir une continuité du métier de l'entreprise, cette dernière doit mettre en place un Plan de Continuité de l'Activité (PCA) sujet en-dehors du scope de cet article. Mettre en place un PCA est un projet à part entière et par conséquent entraîne certainement des investissements et des retombés financières (en termes de rentabilité business) sont également attendus. Donc, afin de justifier le projet, il est naturel de parler de ROI entre autres. Comme le contexte du projet possède un caractère qui a trait à la sécurité les éléments définissant le ROI :
Plus précisément,
![]()
de sorte à ce que la formule du ROI désignée dans ce contexte par ROSI soit donnée par :
![]()
Attention ! Les Gains ne sont pas des profits directs, mais projettent plutôt les montants susceptibles d'être perdus si l'entreprise ne procède pas à investir dans la sécurité. Le coût lié au risque doit refléter la somme des coûts directs ou indirects de l'impact sur le business (la perte en productivité, la perte d'actifs ou de la propriété intellectuelle) et les moyens mis en œuvre en cas de survenance. Le % de réduction du risque doit indiquer le niveau d'atténuation attendu du risque suite à la mise en place de solutions et processus du PCA ou dans le processus continu du maintien en conditions opérationnelles de l'activité. Déterminer ces deux paramètres n'est pas chose facile, car ils concernent des évènements attendus et non avérés ni tangibles. Etant donnés que les incidents relatifs à la sécurité constituent une source des données à utiliser dans l'estimation du ROSI, on peut s'appuyer sur les informations issues des incidents afin d'estimer les différents paramètres à prendre en compte comme nous allons le voir dans l'exemple ci-dessous. Par ailleurs, collecter des données strictement liées à la sécurité et pouvoir estimer les pertes en productivité conséquences directes ou indirectes d'incidents de sécurité n'est pas toujours évident d'une part, et d'autre part, ne constitue pas une préoccupation du premier ordre de toutes les entreprises. Une telle démarche n'est pas encore standardisée et des outils du type ETL capables de collecter, analyser, traiter les données et puis reporter les synthèses existent certainement mais faut-il encore les mettre en œuvre et les industrialiser.
Connaissant le Coût d'exposition au risque et le Coût de l'investissement et en désignant par r le % de réduction du risque et par r0 le ratio (ROI de référence) :
![]()
on peut conclure que :
| • ROSI>0 Si : |
| • ROSI=0 Si : |
| • ROSI<0 Si : |
Afin de mieux comprendre le sens de la formule du ROSI, il n'y a pas mieux qu'un exemple que voici :
Exemple 2 :
Une entreprise souhaite protéger les postes de travail par un antivirus en mettant en place une solution antivirale globale. On suppose que :
Supposons que les virus sont classés en trois niveaux N1, N2 et N3 selon leurs impacts sur le business comme suit :
| Niveau d'impact | Coût lié par virus |
| N1 | 0 |
| N2 | 10000 |
| N3 | 1000000 |
Sur une année 50 000 virus ont été comptabilisés avec une répartition comme suit :
| N de virus total | N de virus niveau 1 | N de virus niveau 2 | N de virus niveau 3 |
| 50000 | 45000 | 4995 | 5 |
| % : | 90,00% | 9,99% | 0,01% |
| Coût d'exposition au risque associé : | 0 | 49 950 000 | 5 000 000 |
Par conséquent le coût moyen pondéré d'exposition au risque est de : 4 990 505€ ! L'éditeur de la solution antivirale estime que le % de réduction du risque est de 70%. Par conséquent le : ROSI = (,70 x 4 990 505 - 1 000 000)/1 000 000 = 249%. Voici deux scénarios que l'entreprise peut envisager :
Scénario 1 : Supposons que l'entreprise étudie plusieurs offres et désire effectuer un comparatif sur la base du taux d'atténuation du risque avancé par l'éditeur. Il est clair que le ROSI croît d'une manière linéaire et croissante par rapport au % de réduction du risque. Le graphe suivant illustre cette constatation et la quantifie :
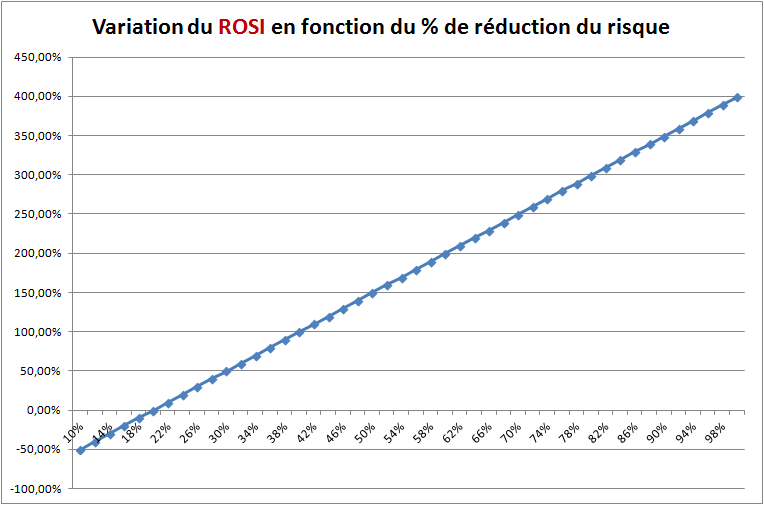
Ci-dessous le même graphe, mais interactif (Glisser-Déplacer la souris dans le sens des axes xy pour ZOOMER):
Scénario 2 : Supposons que l'entreprise veut fixer le % de réduction du risque à au moins 80% et examinons le ROSI en fonction des prix de différentes solutions antivirales. Le graphe ci-dessous illustre la variation du ROSI en fonction du prix de la solution :
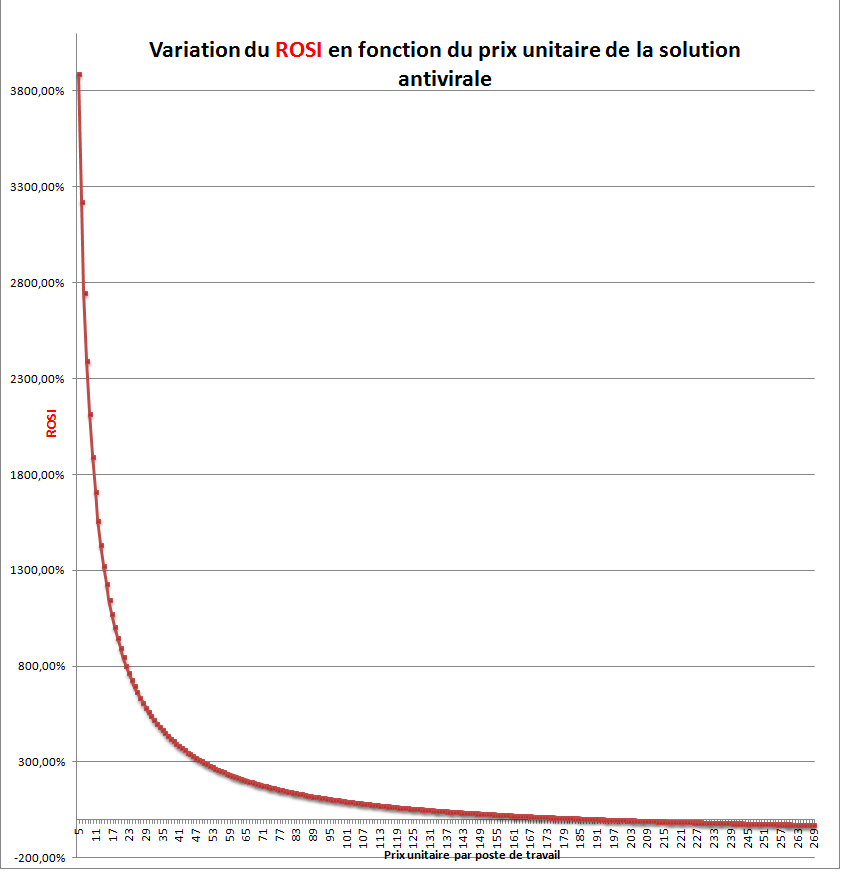
Ci-dessous le même graphe, mais interactif (Glisser-Déplacer la souris dans le sens des axes xy pour ZOOMER):
Sans surprise le ROSI est une fonction décroissante par rapport au prix unitaire de la solution antivirale. le ROI de référence est r0 (%)=1 000 000/4 990 505 =0,200 (équivalent à 20%). Pour un prix unitaire annuel de moins de 200€, le ROSI est positif. A partir d'un coût unitaire de 200€, le ROSI devient nul, voir négatif pour des prix unitaires supérieurs à 200€. Un tel graphe peut fournir une base afin de bien négocier le prix de la solution antivirale avec l'éditeur.
A noter que cet exemple ne reflète pas du tout ce qui se pratique réellement sur le marché des antivirus, il est purement de nature fictive.
Exemple 3 : ROSI vs NPV et IRR (voir mon article QUELQUES NOTIONS DE BASE DE LA FINANCE DES PROJETS à propos des deux dernières métrique), voir la référence indiquée au début de cet article pour les données de l'exemple.
Dans cet exemple on va plutôt se projeter sur une longue période en termes d'investissement (plus de 3 ans) et faire le lien du calcul du ROSI en tant que métrique statique avec les deux métriques dynamiques NPV (Net Present Value) et IRR (Internal Rate of Return) qui ont une dépendance forte du temps. Pour simplifier on suppose que tous les investissements sont réalisés pour une durée de 5 ans avec un taux d'escompte fixe r = 5% à des moments différents selon le scénario indiqué ci-dessous. On suppose que le Coût total d'exposition au risque = 50 000€. Le tableau suivant montre différents scénarios en fonction des coûts dus à des attaques virales bloquées dont les occurrences sont différentes (N°.1 : attaque la 5ème année, N°.2 : attaque la 1ème année, N°.3 : une attaque tous les ans avec un coût de 10 000€ chaque fois):
| Coûts liés à la sécurité antivirale | ||||||||||
| Scénario | Coût de la solution | Année 1 | Année 2 | Année 3 | Année 4 | Année 5 | NPV | IRR | ROI | ROSI |
| N°.1 | -10000 | 0 | 0 | 0 | 0 | 50000 | 27 787 € | 38% | 400% | 250% |
| N°.2 | -10000 | 50000 | 0 | 0 | 0 | 0 | 35 828 € | 400% | 400% | 250% |
| N°.3 | -10000 | 10000 | 10000 | 10000 | 10000 | 10000 | 31 709 € | 97% | 400% | 250% |
| N°.4 | -10000 | 17500 | 15000 | 10000 | 5000 | 2500 | 33 317 € | 153% | 400% | 250% |
Pour chaque scénario les coûts associés aux expositions de risque par année correspondent en termes des finances aux cash-flow entrants. Voici les conclusions :
Le tableau suivant résume le comparatif par rang croissant du plus vers le moins rentable (de 1 à 4) entre les 4 scénarios :
| Scénario | NPV | IRR | ROI | ROSI |
| N°.1 | 4 | 4 | 1 | 1 |
| N°.2 | 1 | 1 | 1 | 1 |
| N°.3 | 3 | 3 | 1 | 1 |
| N°.4 | 2 | 2 | 1 | 1 |
Il montre clairement que Le ROI et le ROSI ne dépendent pas de la répartition des coûts d'exposition au risque, mais uniquement du montant total de ces derniers. La NPV et le IRR sont classés dans le même ordre et fournissent les mêmes conclusions.
Il subsiste néanmoins un paradoxe concernant le meilleur scénario en particulier ! Car on estime que la solution antivirale bloque une attaque ayant comme coût d'exposition de 50K la 1ère année et aucune les années suivantes, alors que les fabricants de virus ou les hackers travaillent aussi pour rendre les attaques plus virulentes et susceptibles de ne pas être arrêtées par les antivirus. Néanmoins, les fournisseurs de solutions antivirales travaillent aussi activement tous les jours y compris la nuit pour assurer une protection optimale des infrastructures et composants de leurs clients.
Par la définition même du ROSI, il est intrinsèquement basé sur des données ayant un caractère d'incertitude. Dans de telle situation, plusieurs tactiques peuvent être envisagées afin de palier aux paramètres inconnus intervenant dans l'évaluation du ROSI. Parmi les méthodes les plus utilisées dans ce cas est celle de Monte Carlo. Sans rentrer dans les détails, voici un exemple qui reprend la même idée que l'exemple 2.
Exemple 3 : Comment déterminer par simulation le Coût de réduction de risque et l'Investissement approprié
Nous reprenons ici l'exemple 2, mais au lieu de se baser sur des données statiques et hypothétiques, nous allons plutôt utiliser des données compilées sur la base de données se rapprochant le plus d'une des distributions utilisées par la méthode Monte Carlo afin de simuler des données historiques. Afin d'illustrer cette démarche, nous les expliquons par un exemple dont les étapes à suivre (applicables dans d'autres contextes aussi) sont les suivantes :
ETAPE 1 :Fixer l'intervalle de variation du nombre de virus de chaque niveau
Voici un tableau contenant des données générées sur une longue période disons 50 ans (voire même 100 ans) en supposant que les données des années sont soumises aux contraintes :
ETAPE 2 : Générer des données sur une certaine durée d'une manière aléatoire
Les données concernant les nombres de virus de chaque niveau, sont générées aléatoirement (ici sur 1000 années !):
| Année | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 1000 |
| N Virus Niveau N1 | 64 577 | 58 638 | 52 617 | 77 419 | 64 539 | 75 204 | 65 806 | 71 372 | 70 420 | 74 910 | ... | 78 854 |
| N Virus Niveau N2 | 14 179 | 14 073 | 11 990 | 15 737 | 12 918 | 17 255 | 19 558 | 13 578 | 10 917 | 16 342 | ... | 10 999 |
| N Virus Niveau N3 | 7 | 8 | 9 | 5 | 10 | 9 | 7 | 10 | 8 | 9 | ... | 10 |
Le tableau suivant (dynamique) reporte à chaque itération les valeurs max, la plus probable et min qui seront utilisées dans la simulation Monte Carlo à l'étape suivante :
| Min | Valeur la plus probable | Max |
| 50 014 | 73 405 | 79 991 |
| 10 011 | 16 605 | 19 995 |
| 5 | 8 | 10 |
A noter que la valeur la plus probable a été définie comme étant 48% x min + 70% x max afin de bien préserver l'ordre des 3 valeurs qui seront utilisées à l'étape suivante.
Il faut bien noter que ces deux tableaux ne sont pas statiques et contiennent des données générées aléatoirement à chaque itération de la méthode Monte Carlo que nous allons aborder à l'étape suivante. En outre, les valeurs moyennes du dernier tableau sont déjà assez proches des résultats des simulations Monte Carlo.
ETAPE 3: Application de la simulation Monte Carlo
Le produit @RISK de PALISADE qui s'intègre dans MS EXCEL en tant que complément, peut être utilisé afin de générer une distribution des 3 types de virus (Niveaux 1, 2 et 3). Pour cela, on peut utiliser par exemple la simulation basée sur la triangulation (dynamique) qui justement requiert trois paramètres : Min, la valeur la plus probable et Max calculés dynamiquement à l'étape 2 (2ème table) pour produire les résultats suivants :
| Simulation d'une itération : | % | Risk Min | Risk Mean | Risk Max | |
| N Virus Niveau N1 | 69 726 | 81,14% | 50 677 | 69 731 | 79 894 |
| N Virus Niveau N2 | 16 198 | 18,85% | 10 160 | 16 199 | 19 930 |
| N Virus Niveau N3 | 8 | 0,01% | 5 | 8 | 10 |
Après un certain nombre de simulations dont les variations des résultats ne dépassent pas 0,05% pour tous les niveaux, il en résulte que la répartition des 3 niveaux de virus demeure stable avec une marge d'erreur assez faible et dont la moyenne est la suivante :
| Résultat de la Simulation : | Nombre | % |
| N Virus Niveau N1 | 69 720 | 81,14% |
| N Virus Niveau N2 | 16 200 | 18,85% |
| N Virus Niveau N3 | 8 | 0,01% |
Avec ces estimations en %, il est tout-à-fait possible de calculer le ROSI en fonction du nombre de virus susceptibles d'être contractés par année tout en restant dans les intervalles de la simulation : [50 000 à 80 000] pour le niveau 1, [10 000 à 20 000] pour le niveau 2 et [5 à 10] pour le niveau 3, autrement dit avec un total de virus qui est situé dans l'intervalle [60 000, 100 000].
Les graphes suivants illustrent les simulations Monte Carlo des 3 métriques :
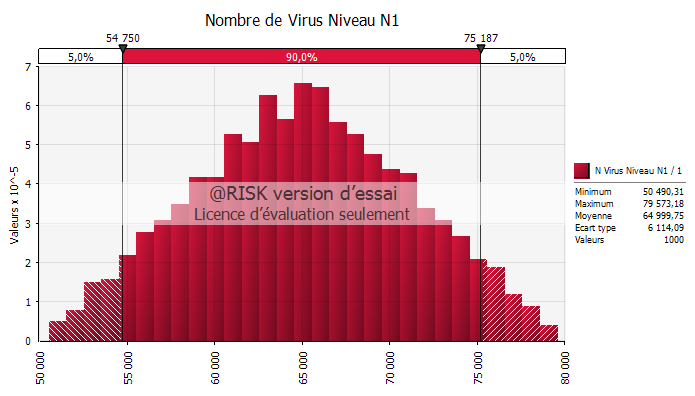
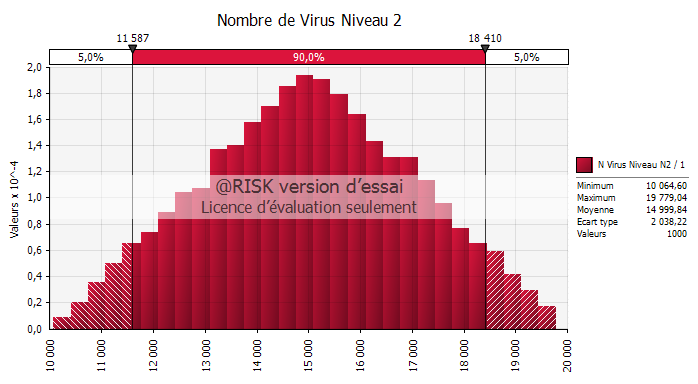
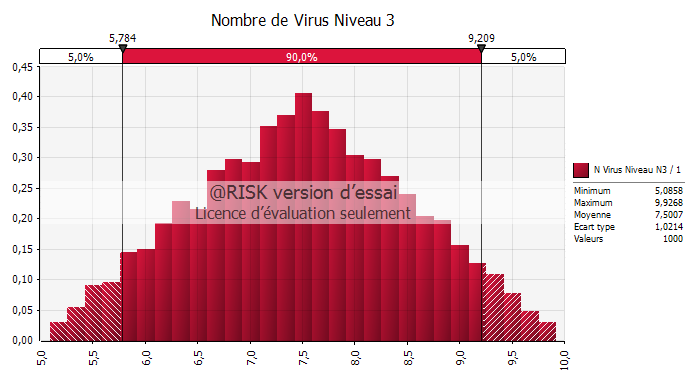
Il est temps maintenant d'attaquer la partie sensible, car nous allons parler finance. Plus précisément, à partir des éléments obtenus ci-dessus, on peut résumer les coûts dans le tableau suivant :
| Coût par virus | Coût total Max |
Taux de virulence |
Coût total normalisé* |
Coût total résiduel après atténuation du risque de 98%** |
|
| Virus Niveau 1 | 0 € | 0 € | 0% | 0 € | 0 € |
| Virus Niveau 2 | 10 000 € | 149 853 339 € | 2% | 2 997 067 € | 59 941 € |
| Virus Niveau 3 | 1 000 000 € | 7 506 900 € | 50% | 3 753 450 € | 75 069 € |
| Coût Total : | 1 010 000 € | 157 360 239 € | 6 750 517 € | 135 010 € |
*Le coût total normalisé correspond à 0%, 2% et 50% des virus du niveau 1, 2 et 3 respectivement. Ceci correspond à la probabilité pour que le virus impacte le business de l'entreprise et engendre des pertes financières.
**Voir le tableau ci-dessous pour un % d'atténuation de risque quelconque.
Le tableau suivant illustre la variation du ROSI et du Coût résiduel de l'exposition au risque en fonction du % de réduction du risque :
| % de réduction du risque |
ROSI | Coût résiduel de l'exposition au risque |
| 4% | -73,27% | 6 480 496 € |
| 6% | -59,90% | 6 345 486 € |
| 8% | -46,53% | 6 210 475 € |
| 10% | -33,16% | 6 075 465 € |
| 12% | -19,80% | 5 940 455 € |
| 14% | -6,43% | 5 805 444 € |
| 16% | 6,94% | 5 670 434 € |
| 18% | 20,31% | 5 535 424 € |
| 20% | 33,67% | 5 400 413 € |
| 22% | 47,04% | 5 265 403 € |
| 24% | 60,41% | 5 130 393 € |
| 26% | 73,78% | 4 995 382 € |
| 28% | 87,14% | 4 860 372 € |
| 30% | 100,51% | 4 725 362 € |
| 32% | 113,88% | 4 590 351 € |
| 34% | 127,25% | 4 455 341 € |
| 36% | 140,61% | 4 320 331 € |
| 38% | 153,98% | 4 185 320 € |
| 40% | 167,35% | 4 050 310 € |
| 42% | 180,71% | 3 915 300 € |
| 44% | 194,08% | 3 780 289 € |
| 46% | 207,45% | 3 645 279 € |
| 48% | 220,82% | 3 510 269 € |
| 50% | 234,18% | 3 375 258 € |
| 52% | 247,55% | 3 240 248 € |
| 54% | 260,92% | 3 105 238 € |
| 56% | 274,29% | 2 970 227 € |
| 58% | 287,65% | 2 835 217 € |
| 60% | 301,02% | 2 700 207 € |
| 62% | 314,39% | 2 565 196 € |
| 64% | 327,76% | 2 430 186 € |
| 66% | 341,12% | 2 295 176 € |
| 68% | 354,49% | 2 160 165 € |
| 70% | 367,86% | 2 025 155 € |
| 72% | 381,22% | 1 890 145 € |
| 74% | 394,59% | 1 755 134 € |
| 76% | 407,96% | 1 620 124 € |
| 78% | 421,33% | 1 485 114 € |
| 80% | 434,69% | 1 350 103 € |
| 82% | 448,06% | 1 215 093 € |
| 84% | 461,43% | 1 080 083 € |
| 86% | 474,80% | 945 072 € |
| 88% | 488,16% | 810 062 € |
| 90% | 501,53% | 675 052 € |
| 92% | 514,90% | 540 041 € |
| 94% | 528,27% | 405 031 € |
| 96% | 541,63% | 270 021 € |
| 98% | 555,00% | 135 010 € |
| 100% | 568,37% | 0 € |
Un % de réduction du risque d'au moins 85% semble être le plus approprié pour notre investissement de 1 010 000€ (voir lignes bleu dans le tableau) auquel cas le ROSI correspondant est d'au moins 468%. Les deux graphes suivants correspondent aux variations du ROSI et du coût résiduel de l'exposition au risque en fonction du % de réduction du risque :
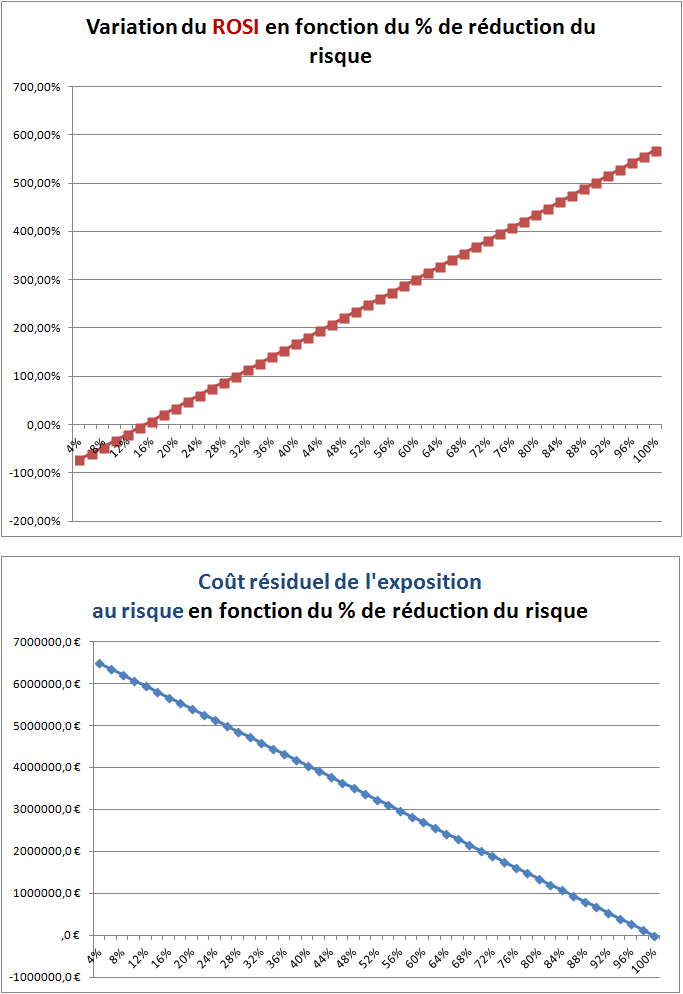
Pour simplifier, on suppose que le coût relatif à la réduction du risque est réparti d'une manière égalitaire sur une durée de 5 ans avec un taux d'escompte fixé à 5%. Le tableau calcule en plus du ROSI, la NPV et le IRR afin de bien analyser le projet d'investissement en s'appuyant non seulement sur le ROSI, mais aussi sur d'autres indicateurs d'aide à la décision. Pour plus de détails sur le NPV et le IRR, vous pouvez consulter mon article : QUELQUES NOTIONS DE BASE DE LA FINANCE DES PROJETS.
| % de réduction du risque |
ROSI | Coût résiduel de l'exposition au risque |
Investissement | Année 1 | Année 2 | Année 3 | Année 4 | Année 5 | NPV | IRR |
| 4% | -73% | 6 480 496 € | -1 010 000 € | 1 296 099 € | 1 296 099 € | 1 296 099 € | 1 296 099 € | 1 296 099 € | 4 601 431 € | 126% |
| 6% | -60% | 6 345 486 € | -1 010 000 € | 1 269 097 € | 1 269 097 € | 1 269 097 € | 1 269 097 € | 1 269 097 € | 4 484 527 € | 123% |
| 8% | -47% | 6 210 475 € | -1 010 000 € | 1 242 095 € | 1 242 095 € | 1 242 095 € | 1 242 095 € | 1 242 095 € | 4 367 622 € | 121% |
| 10% | -33% | 6 075 465 € | -1 010 000 € | 1 215 093 € | 1 215 093 € | 1 215 093 € | 1 215 093 € | 1 215 093 € | 4 250 717 € | 118% |
| 12% | -20% | 5 940 455 € | -1 010 000 € | 1 188 091 € | 1 188 091 € | 1 188 091 € | 1 188 091 € | 1 188 091 € | 4 133 812 € | 115% |
| 14% | -6% | 5 805 444 € | -1 010 000 € | 1 161 089 € | 1 161 089 € | 1 161 089 € | 1 161 089 € | 1 161 089 € | 4 016 907 € | 112% |
| 16% | 7% | 5 670 434 € | -1 010 000 € | 1 134 087 € | 1 134 087 € | 1 134 087 € | 1 134 087 € | 1 134 087 € | 3 900 002 € | 110% |
| 18% | 20% | 5 535 424 € | -1 010 000 € | 1 107 085 € | 1 107 085 € | 1 107 085 € | 1 107 085 € | 1 107 085 € | 3 783 098 € | 107% |
| 20% | 34% | 5 400 413 € | -1 010 000 € | 1 080 083 € | 1 080 083 € | 1 080 083 € | 1 080 083 € | 1 080 083 € | 3 666 193 € | 104% |
| 22% | 47% | 5 265 403 € | -1 010 000 € | 1 053 081 € | 1 053 081 € | 1 053 081 € | 1 053 081 € | 1 053 081 € | 3 549 288 € | 101% |
| 24% | 60% | 5 130 393 € | -1 010 000 € | 1 026 079 € | 1 026 079 € | 1 026 079 € | 1 026 079 € | 1 026 079 € | 3 432 383 € | 98% |
| 26% | 74% | 4 995 382 € | -1 010 000 € | 999 076 € | 999 076 € | 999 076 € | 999 076 € | 999 076 € | 3 315 478 € | 95% |
| 28% | 87% | 4 860 372 € | -1 010 000 € | 972 074 € | 972 074 € | 972 074 € | 972 074 € | 972 074 € | 3 198 574 € | 93% |
| 30% | 101% | 4 725 362 € | -1 010 000 € | 945 072 € | 945 072 € | 945 072 € | 945 072 € | 945 072 € | 3 081 669 € | 90% |
| 32% | 114% | 4 590 351 € | -1 010 000 € | 918 070 € | 918 070 € | 918 070 € | 918 070 € | 918 070 € | 2 964 764 € | 87% |
| 34% | 127% | 4 455 341 € | -1 010 000 € | 891 068 € | 891 068 € | 891 068 € | 891 068 € | 891 068 € | 2 847 859 € | 84% |
| 36% | 141% | 4 320 331 € | -1 010 000 € | 864 066 € | 864 066 € | 864 066 € | 864 066 € | 864 066 € | 2 730 954 € | 81% |
| 38% | 154% | 4 185 320 € | -1 010 000 € | 837 064 € | 837 064 € | 837 064 € | 837 064 € | 837 064 € | 2 614 049 € | 78% |
| 40% | 167% | 4 050 310 € | -1 010 000 € | 810 062 € | 810 062 € | 810 062 € | 810 062 € | 810 062 € | 2 497 145 € | 75% |
| 42% | 181% | 3 915 300 € | -1 010 000 € | 783 060 € | 783 060 € | 783 060 € | 783 060 € | 783 060 € | 2 380 240 € | 72% |
| 44% | 194% | 3 780 289 € | -1 010 000 € | 756 058 € | 756 058 € | 756 058 € | 756 058 € | 756 058 € | 2 263 335 € | 70% |
| 46% | 207% | 3 645 279 € | -1 010 000 € | 729 056 € | 729 056 € | 729 056 € | 729 056 € | 729 056 € | 2 146 430 € | 67% |
| 48% | 221% | 3 510 269 € | -1 010 000 € | 702 054 € | 702 054 € | 702 054 € | 702 054 € | 702 054 € | 2 029 525 € | 64% |
| 50% | 234% | 3 375 258 € | -1 010 000 € | 675 052 € | 675 052 € | 675 052 € | 675 052 € | 675 052 € | 1 912 620 € | 61% |
| 52% | 248% | 3 240 248 € | -1 010 000 € | 648 050 € | 648 050 € | 648 050 € | 648 050 € | 648 050 € | 1 795 716 € | 58% |
| 54% | 261% | 3 105 238 € | -1 010 000 € | 621 048 € | 621 048 € | 621 048 € | 621 048 € | 621 048 € | 1 678 811 € | 55% |
| 56% | 274% | 2 970 227 € | -1 010 000 € | 594 045 € | 594 045 € | 594 045 € | 594 045 € | 594 045 € | 1 561 906 € | 51% |
| 58% | 288% | 2 835 217 € | -1 010 000 € | 567 043 € | 567 043 € | 567 043 € | 567 043 € | 567 043 € | 1 445 001 € | 48% |
| 60% | 301% | 2 700 207 € | -1 010 000 € | 540 041 € | 540 041 € | 540 041 € | 540 041 € | 540 041 € | 1 328 096 € | 45% |
| 62% | 314% | 2 565 196 € | -1 010 000 € | 513 039 € | 513 039 € | 513 039 € | 513 039 € | 513 039 € | 1 211 192 € | 42% |
| 64% | 328% | 2 430 186 € | -1 010 000 € | 486 037 € | 486 037 € | 486 037 € | 486 037 € | 486 037 € | 1 094 287 € | 39% |
| 66% | 341% | 2 295 176 € | -1 010 000 € | 459 035 € | 459 035 € | 459 035 € | 459 035 € | 459 035 € | 977 382 € | 35% |
| 68% | 354% | 2 160 165 € | -1 010 000 € | 432 033 € | 432 033 € | 432 033 € | 432 033 € | 432 033 € | 860 477 € | 32% |
| 70% | 368% | 2 025 155 € | -1 010 000 € | 405 031 € | 405 031 € | 405 031 € | 405 031 € | 405 031 € | 743 572 € | 29% |
| 72% | 381% | 1 890 145 € | -1 010 000 € | 378 029 € | 378 029 € | 378 029 € | 378 029 € | 378 029 € | 626 667 € | 25% |
| 74% | 395% | 1 755 134 € | -1 010 000 € | 351 027 € | 351 027 € | 351 027 € | 351 027 € | 351 027 € | 509 763 € | 22% |
| 76% | 408% | 1 620 124 € | -1 010 000 € | 324 025 € | 324 025 € | 324 025 € | 324 025 € | 324 025 € | 392 858 € | 18% |
| 78% | 421% | 1 485 114 € | -1 010 000 € | 297 023 € | 297 023 € | 297 023 € | 297 023 € | 297 023 € | 275 953 € | 14% |
| 80% | 435% | 1 350 103 € | -1 010 000 € | 270 021 € | 270 021 € | 270 021 € | 270 021 € | 270 021 € | 159 048 € | 11% |
| 82% | 448% | 1 215 093 € | -1 010 000 € | 243 019 € | 243 019 € | 243 019 € | 243 019 € | 243 019 € | 42 143 € | 6% |
| 84% | 461% | 1 080 083 € | -1 010 000 € | 216 017 € | 216 017 € | 216 017 € | 216 017 € | 216 017 € | -74 761 € | 2% |
| 86% | 475% | 945 072 € | -1 010 000 € | 189 014 € | 189 014 € | 189 014 € | 189 014 € | 189 014 € | -191 666 € | -2% |
| 88% | 488% | 810 062 € | -1 010 000 € | 162 012 € | 162 012 € | 162 012 € | 162 012 € | 162 012 € | -308 571 € | -7% |
| 90% | 502% | 675 052 € | -1 010 000 € | 135 010 € | 135 010 € | 135 010 € | 135 010 € | 135 010 € | -425 476 € | -12% |
| 92% | 515% | 540 041 € | -1 010 000 € | 108 008 € | 108 008 € | 108 008 € | 108 008 € | 108 008 € | -542 381 € | -18% |
| 94% | 528% | 405 031 € | -1 010 000 € | 81 006 € | 81 006 € | 81 006 € | 81 006 € | 81 006 € | -659 286 € | -24% |
| 96% | 542% | 270 021 € | -1 010 000 € | 54 004 € | 54 004 € | 54 004 € | 54 004 € | 54 004 € | -776 190 € | - |
| 98% | 555% | 135 010 € | -1 010 000 € | 27 002 € | 27 002 € | 27 002 € | 27 002 € | 27 002 € | -893 095 € | - |
| 100% | 568% | 0 € | -1 010 000 € | 0 € | 0 € | 0 € | 0 € | 0 € | -1 010 000 € | - |
La ligne verte du tableau correspond à la situation optimale sous les conditions d'investissement annoncées au début sur tous les plans, car :
Voici un exemple y compris les résultats de la similation Monte Carlo que vous pouvez tester en utilisant l'outil @RISK PALISADE :
Données et Paramètres (à noter que la valeur la plus probable peut être identique au MIN ou au MAX) :
| Paramètres : | MIN | MAX | La plus probable (50% x MIN + 70% x MAX) | Répartition (%) |
| Niveau 1 | 500 000 | 1 000 000 | 1 000 000 | 70,17% |
| Niveau 2 | 100 000 | 500 000 | 425 000 | 29,82% |
| Niveau 3 | 10 | 100 | 80 | 0,01% |
L'application de la méthode Monte Carlo (avec 2000 itérations et 10 simulations) via une triangulation utilisant les 3 paramètres indiqués dans le tableau ci-dessus, produit le résultat suivant :
| Résultats : | Nombre | % | Marge d'erreur MAX | Risk Min | Risk Mean | Risk Max | Risk stdev |
| Niveau N1 | 816 725 | 71,01% | 0,06% | 509 878 | 816 640 | 998 974 | 112 259 |
| Niveau N2 | 333 337 | 28,98% | 0,06% | 107 944 | 333 307 | 495 800 | 84 830 |
| Niveau N3 | 62 | 0,01% | 0,06% | 12 | 62 | 99 | 19 |
En axaminant la formule qui fournit le ROSI nous constatons que le terme exprimant les gains est fonction de deux éléments déterminants : le % de réduction des risques et le Coût d'exposition au risque. Or ces deux facteurs ne sont pas généralement identiques pour des risques n'ayant pas le même niveau d'impact sur le business et dans la pratique ne peuvent pas être calculés d'une manière unique. Ceci suggère une reformulation plus fine et plus générale comme suit :
![]()
avec :
| Coût d'exposition au risque pour l'élément i. | |
| Pourcentage de réduction de risque pour l'élément i. | |
| N : | Nombre d'élément concernés par l'investissement. Il peut s'agit de plusieurs classes de risques ou de catégiries. |
Voici un exemple simple reprenant l'exemple 2 précédent sur lequel nous appliquons la nouvelle formule du ROSI.
Exemple 4 : N=3 catégories
Le tableau suivant indique les 3 catégories de virus selon leur impact sur le business :
|
Catégorie du risque (selon le niveau) |
Nombre | % | Coût de perte par virus contracté | Cer | Prr |
| Virus Niveau 1 | 65 003 | 81,26% | 0 | 0 | 99% |
| Virus Niveau 2 | 14 985 | 18,73% | 100 | 100 x 14 985 | 95% |
| Virus Niveau 3 | 8 | 0,01% | 10 000 | 10 000 x 8 | 50% |
En appliquant la formule du ROSI, on a :
![]()
Autrement dit, ROSI = 46%.
En conclusion, on a vu à travers des exemples que le calcul du ROSI est beaucoup plus complexe que la quantification des autres indicateurs décisionnels comme le ROI, la NPV ou le IRR. L'utilisation de la méthode Monte Carlo s'avère efficace à condition de disposer d'un certain nombre d'informations indispensables pour dérouler des simulations et ainsi arriver à des conclusions tangibles. Une méthode a été présentée dans un cas spécifique afin d'aboutir à modéliser les données et appliquer la méthode Monte Carlo. Cette méthode peut être facilement adaptée en fonction du contexte et de la problématique à traiter.